YZOJ P3706 [APIO2018]新家

时间限制：5000MS 内存限制：1048576KB

难度： $7.0$

题目描述

五福街是一条笔直的道路，这条道路可以看成一个数轴，街上每个建筑物的坐标都可以用一个整数来表示。

小明是一位时光旅行者，他知道在这条街上，在过去现在和未来共有 $n$ 个商店出现。第 $i$ 个商店可以使用四个整数 $x_i , t_i , a_i , b_i$ 描述，它们分别表示：商店的坐标、商店的类型、商店开业的年份、商店关闭的年份。

小明希望通过时光旅行，选择一个合适的时间，住在五福街上的某个地方。他给出了一份他可能选择的列表，上面包括了 $q$ 个询问，每个询问用二元组（坐标，时间）表示。第 $i$ 对二元组用两个整数 $l_i , y_i$ 描述，分别表示选择的地点 $l_i$ 和年份 $y_i$ 。

现在，他想计算出在这些时间和地点居住的生活质量。他定义居住的不方便指数为：在居住的年份，离居住点最远的商店类型到居住点的距离。类型 $t$ 的商店到居住点的距离定义为：在指定的年份，类型 $t$ 的所有营业的商店中，到居住点距离最近的一家到居住点的距离。我们说编号为 $i$ 的商店在第 $y$ 年在营业当且仅当 $a_i \leq y \leq b_i$ 。注意，在某些年份中，可能在五福街上并非所有 $k$ 种类型的商店都有至少一家在营业。在这种情况下，不方便指数定义为 $-1$ 。

你的任务是帮助小明求出每对（坐标，时间）二元组居住的不方便指数。

输入格式

第一行包含三个整数 $n,k$ 和 $q$ ，分别表示商店的数量、商店类型的数量和（坐标，时间）二元组的数量（ $1 \le n, q \le 3 \times 10^5 , 1 \le k \le n$ ）

接下来 $n$ 行，每行包含四个整数 $x_i , t_i , a_i$ 和 $b_i$ 用于描述一家商店，意义如题面所述（ $1 \le x_i , a_i , b_i \le 10^8 , 1 \le t_i \le k, a_i \le b_i$ ）。

接下来 $q$ 行，每行包含两个整数 $l_i$ 和 $y_i$ ，表示一组（坐标，时间）查询（ $1 \le l_i , y_i \leq 10^8$ ）。

输出格式

输出一行，包含 $q$ 个整数，依次表示对于 $q$ 组（坐标，时间）询问求出的结果。

样例 1 输入

4 2 4

3 1 1 10

9 2 2 4

7 2 5 7

4 1 8 10

5 3

5 6

5 9

1 10

样例 1 输出

4
2
-1
-1

-1

样例 1 说明

在第一个样例中，有 $4$ 家商店，共 $2$ 种类型，还有 $4$ 个询问。

• 对于第一个询问：小明在第 $3$ 年住在坐标为 $5$ 的地方。这一年中，编号为 $1$ 和 $2$ 的商店在营业，到编号为 $1$ 的商店的距离为 $2$ ，到编号为 $2$ 的商店距离为 $4$ ，所以最大距离为 $4$ 。

• 对于第二个询问：小明在第 $6$ 年住在坐标为 $5$ 的地方。这一年中，编号为 $1$ 和 $3$ 的商店在营业，到编号为 $1$ 的商店的距离为 $2$ ，到编号为 $3$ 的商店距离为 $2$ ，所以最大距离为 $2$ 。

• 对于第三个询问：小明在第 $9$ 年住在坐标为 $5$ 的地方。这一年中，编号为 $1$ 和 $4$ 的商店在营业，它们的类型都为 $1$ ，没有类型为 $2$ 的商店在营业，所以答案为 $-1$ 。

• 同样的情况出现在第四个询问中。

其实很简单，就是DataStructure大力维护操作。

首先按照时间离散化，分成三种类型：出现，消失，询问。

对于一个询问 $x$ ，可以想到二分答案 $mid$ 表示 $[x-mid, x+mid]$ 中是否存在所有类型的商店。

由于只要判断是否存在，所以可以记录 $pre_x$ 表示位于 $x$ 坐标的商店往左第一个出现的同种类型的商店（不包括重复）。

假设 $-\infty$ 和 $+\infty$ 处有所有类型的商店，那么：

$[l, r]$ 中存在所有类型的商店，其实等价于 $\min\limits_{x=r+1}^{+\infty}{pre_x} \geq l$ ，因为 $(pre_x, x)$ 中不存在这种类型的商店。

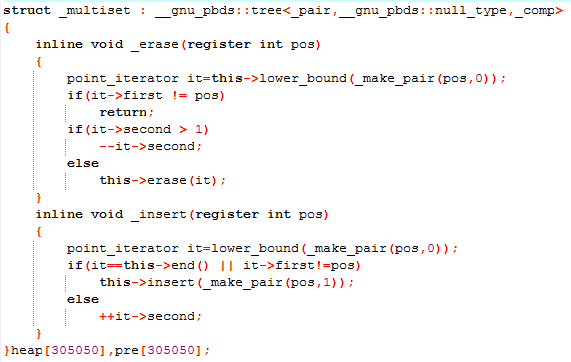
$pre$ 使用全局线段树维护（动态开点/离散化均可），由于有删除（修改）操作，所以对每个叶子结点维护一个可删堆（或 multiset）。

还有，由于增加删除商店的时候，会对某个坐标的后继的 $pre$ 产生影响，所以对每种类型的商店都维护一个 multiset 支持查找前驱后继。

暴力二分线段树判断是 $O(nlog^2n)$ ，套在一起就可以 $O(nlogn)$ 。

具体来说就是对于线段树上一段区间 $[l, r]$ ：如果 $pos > mid$ 那么答案区间的右端点肯定在右半边，往右走；否则考虑 $mid$ 是否能作为答案区间的右端点，若可以即 $\min\limits_{x=mid+1}^{+\infty} {pre_x} \geq pos-\left(mid-pos\right)$ 那么肯定往左走更优，否则也只能向右走。

这个东西（指 $\min\limits_{x=mid+1}^{+\infty} {pre_x}$ ）很明显向左走的时候 $mid$ 是单调递减的，又由于是在线段树上，所以只需要在往左走的时候维护即可。

最后在线段树上二分出来的 $ans$ 是答案区间的右端点，要求的答案为 $mid=ans-pos$ 。

// std::multiset time test
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <climits>
#include <algorithm>
#include <set>

#define _min(_a_,_b_) ((_a_)<(_b_)?(_a_):(_b_))
#define _max(_a_,_b_) ((_a_)>(_b_)?(_a_):(_b_))

#ifdef ONLINE_JUDGE
	char __B[1<<15],*__S=__B,*__T=__B;
	#define getchar() (__S==__T&&(__T=(__S=__B)+fread(__B,1,1<<15,stdin),__S==__T)?EOF:*__S++)
#endif
inline int getnum()
{
	register char c=0;
	while(!(c>='0' && c<='9'))
		c=getchar();
	register int a=0;
	while(c>='0' && c<='9')
		a=a*10+c-'0',c=getchar();
	return a;
}

inline void printnum(register int a)
{
	if(a<0)
		putchar('-'),a=-a;
	static char buf[64];buf[0]=0;
	register int top=0;
	while(a)
		buf[top++]=a%10,a/=10;
	for(register int i=_max(top-1,0);i>=0;i--)
		putchar(buf[i]+'0');
}

struct _multiset : std::multiset<int>
{
	inline void _erase(register int pos)
	{
		iterator it=this->find(pos);
		if(it != this->end())
			this->erase(it);
	}
	inline void _insert(register int pos)
	{
		this->insert(pos);
	}
}heap[305050],pre[305050];

#define _TSIZE 10505050
int cnt,lson[_TSIZE],rson[_TSIZE],mnv[_TSIZE],root;
int icnt,idxmap[_TSIZE];
#define _LMIN (0)
#define _LMAX (2e8+1)

#define PushUp(_o) \
{ \
	mnv[_o]=_min(mnv[lson[_o]],mnv[rson[_o]]); \
}

int MP,MD,MA;
void ModifyTree(int&o,register int l=_LMIN,register int r=_LMAX)
{
	if(!o)
		o=++cnt;
	if(l == r)
	{
		register int x=idxmap[o];
		if(!x)
			x=idxmap[o]=++icnt;
		if(MA>=0)
			heap[x]._insert(MA);
		if(MD>=0)
			heap[x]._erase(MD);
			
		mnv[o]=(heap[x].size() ? *heap[x].begin() : _LMAX);
		return;
	}
	register int mid=(l+r)>>1;
	if(MP <= mid)
		ModifyTree(lson[o],l,mid);
	else
		ModifyTree(rson[o],mid+1,r);
	PushUp(o);
}

int QueryTreeE(register int pos)
{
	register int o=root,l=_LMIN,r=_LMAX,mv=r;
	while(l<r)
	{
		register int mid=(l+r)>>1,nmv=_min(mv,mnv[rson[o]]);
		if(pos>mid || nmv<1 || mid+nmv<(pos<<1))
			l=mid+1,o=rson[o];
		else
			r=mid,o=lson[o],mv=nmv;
	}
	return l-pos;
}

struct _query
{
	short opt;
	int x,t,y;
	bool operator < (const _query&o)const
	{
		if(y != o.y)
			return y<o.y;
		return opt<o.opt;
	}
}query[905050];
int ans[305050];

int main()
{
	register int N=getnum(),K=getnum(),Q=getnum();
	register int lq=0;
	for(register int i=1;i<=N;i++)
	{
		query[++lq]=(_query){1,getnum(),getnum(),getnum()};
		++lq,query[lq]=query[lq-1];
		query[lq].opt=2,query[lq].y=getnum()+1;
	}
	for(register int i=1;i<=Q;i++)
		query[++lq]=(_query){3,getnum(),i,getnum()};
	std::sort(&query[1],&query[lq+1]);
	
	for(register int i=1;i<=K;i++)
		pre[i]._insert(_LMIN),pre[i]._insert(_LMAX);
	mnv[0]=INT_MAX;
	MP=_LMAX,MA=_LMIN,MD=-1,ModifyTree(root);
	
	register int tcnt=0;
	for(register int i=1;i<=lq;i++)
		//if(printf("%d: %d %d %d %d\n",i,query[i].opt,query[i].x,query[i].t,query[i].y)<0);
		if(query[i].opt == 3)
			ans[query[i].t]=(tcnt==K ? QueryTreeE(query[i].x) : -1);
		else if(query[i].opt == 1)
		{
			register int x=query[i].x,t=query[i].t;
			_multiset::iterator dit=pre[t].lower_bound(x),it=dit--;
			MP=*it,MA=x,MD=*dit,ModifyTree(root);
			//printf("modify %d %d %d\n",MP,MA,MD);
			MP=x,MA=*dit,MD=-1,ModifyTree(root);
			//printf("modify %d %d %d\n",MP,MA,MD);
			if(pre[t].size() == 2)
				tcnt++;
			pre[t]._insert(x);
		}
		else if(query[i].opt == 2)
		{
			register int x=query[i].x,t=query[i].t;
			pre[t]._erase(x);
			if(pre[t].size() == 2)
				tcnt--;
			_multiset::iterator dit=pre[t].lower_bound(x),it=dit--;
			MP=x,MA=-1,MD=*dit,ModifyTree(root);
			//printf("modify %d %d %d\n",MP,MA,MD);
			MP=*it,MA=*dit,MD=x,ModifyTree(root);
			//printf("modify %d %d %d\n",MP,MA,MD);
			
		}
	for(register int i=1;i<=Q;i++)
		printnum(ans[i]),putchar('\n');
	
	return 0;
}

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

167

168

169

170

// std::multiset time test

#include <cstdio>

#include <cstdlib>

#include <cstring>

#include <climits>

#include <algorithm>

#include <set>

#define _min(_a_,_b_) ((_a_)<(_b_)?(_a_):(_b_))

#define _max(_a_,_b_) ((_a_)>(_b_)?(_a_):(_b_))

#ifdef ONLINE_JUDGE

char __B[1<<15],*__S=__B,*__T=__B;

#define getchar() (__S==__T&&(__T=(__S=__B)+fread(__B,1,1<<15,stdin),__S==__T)?EOF:*__S++)

#endif

inline int getnum()

{

while(!(c>='0' && c<='9'))

c=getchar();

while(c>='0' && c<='9')

a=a*10+c-'0',c=getchar();

return a;

}

inline void printnum(register int a)

{

if(a<0)

putchar('-'),a=-a;

static char buf[64];buf[0]=0;

while(a)

buf[top++]=a%10,a/=10;

for(register int i=_max(top-1,0);i>=0;i--)

putchar(buf[i]+'0');

}

struct _multiset : std::multiset<int>

{

inline void _erase(register int pos)

{

iterator it=this->find(pos);

if(it != this->end())

this->erase(it);

}

inline void _insert(register int pos)

{

this->insert(pos);

}

}heap[305050],pre[305050];

#define _TSIZE 10505050

int cnt,lson[_TSIZE],rson[_TSIZE],mnv[_TSIZE],root;

int icnt,idxmap[_TSIZE];

#define _LMIN (0)

#define _LMAX (2e8+1)

#define PushUp(_o) \

{ \

mnv[_o]=_min(mnv[lson[_o]],mnv[rson[_o]]); \

}

int MP,MD,MA;

void ModifyTree(int&o,register int l=_LMIN,register int r=_LMAX)

{

if(!o)

o=++cnt;

if(l == r)

{

if(!x)

x=idxmap[o]=++icnt;

if(MA>=0)

heap[x]._insert(MA);

if(MD>=0)

heap[x]._erase(MD);

mnv[o]=(heap[x].size() ? *heap[x].begin() : _LMAX);

return;

}

if(MP <= mid)

ModifyTree(lson[o],l,mid);

else

ModifyTree(rson[o],mid+1,r);

PushUp(o);

}

int QueryTreeE(register int pos)

{

while(l<r)

{

if(pos>mid || nmv<1 || mid+nmv<(pos<<1))

l=mid+1,o=rson[o];

else

r=mid,o=lson[o],mv=nmv;

}

return l-pos;

}

struct _query

{

short opt;

int x,t,y;

bool operator < (const _query&o)const

{

if(y != o.y)

return y<o.y;

return opt<o.opt;

}

}query[905050];

int ans[305050];

int main()

{

for(register int i=1;i<=N;i++)

{

query[++lq]=(_query){1,getnum(),getnum(),getnum()};

++lq,query[lq]=query[lq-1];

query[lq].opt=2,query[lq].y=getnum()+1;

}

for(register int i=1;i<=Q;i++)

query[++lq]=(_query){3,getnum(),i,getnum()};

std::sort(&query[1],&query[lq+1]);

for(register int i=1;i<=K;i++)

pre[i]._insert(_LMIN),pre[i]._insert(_LMAX);

mnv[0]=INT_MAX;

MP=_LMAX,MA=_LMIN,MD=-1,ModifyTree(root);

for(register int i=1;i<=lq;i++)

//if(printf("%d: %d %d %d %d\n",i,query[i].opt,query[i].x,query[i].t,query[i].y)<0);

if(query[i].opt == 3)

ans[query[i].t]=(tcnt==K ? QueryTreeE(query[i].x) : -1);

else if(query[i].opt == 1)

{

_multiset::iterator dit=pre[t].lower_bound(x),it=dit--;

MP=*it,MA=x,MD=*dit,ModifyTree(root);

//printf("modify %d %d %d\n",MP,MA,MD);

MP=x,MA=*dit,MD=-1,ModifyTree(root);

//printf("modify %d %d %d\n",MP,MA,MD);

if(pre[t].size() == 2)

tcnt++;

pre[t]._insert(x);

}

else if(query[i].opt == 2)

{

pre[t]._erase(x);

if(pre[t].size() == 2)

tcnt--;

_multiset::iterator dit=pre[t].lower_bound(x),it=dit--;

MP=x,MA=-1,MD=*dit,ModifyTree(root);

//printf("modify %d %d %d\n",MP,MA,MD);

MP=*it,MA=*dit,MD=x,ModifyTree(root);

//printf("modify %d %d %d\n",MP,MA,MD);

}

for(register int i=1;i<=Q;i++)

printnum(ans[i]),putchar('\n');

return 0;

}

草还有为什么我的 std::multiset 比 __gnu_pbds::tree 还快

YZOJ P3706 [APIO2018]新家

题目描述

输入格式

输出格式

样例 1 输入

样例 1 输出

样例 1 说明

发表回复 取消回复

发表回复取消回复