YZOJ P3791 餐馆
时间限制:2000MS 内存限制:524288KB
难度:\(6.0\)
-
题目描述
在一条东西向的街道上有 \(n\) 个餐馆,从西向东编号为 \(1\) 至 \(n\),第 \(i\) 个餐馆和第 \(i+1\) 个餐馆的距离为 \(a_i\) 。
吃货小W喜欢到这条街道的餐馆里吃饭。现在,小W得到了 \(m\) 张餐票,每张餐票可以用于在街道上的任一餐馆里吃一餐。在第 \(i\) 个餐馆中,使用第 \(j\) 张餐票吃饭,可以获得的美味度为 \(b_{i,j}\) 。注意,每张餐票最多用一次,但在同一餐馆内可以使用任意多张餐票。
小W打算用完这 \(m\) 张餐票。他可以选择任一餐馆作为起点,每次吃饭时,可以选择一个餐馆,然后从当前位置(上次吃饭的地点,如果不存在则为起点)出发前往该餐馆并用任意一张未用过的餐票吃一餐,直到吃完 \(m\) 餐为止。小W希望最大化每次吃饭的美味度之和减去路上经过的总路程的值。
-
输入格式
输入第一行包含两个正整数 \(n,m\) 。
第二行包含 \(n-1\) 个正整数 \(a_1,a_2,\cdots,a_{n-1}\) 。
接下来 \(n\) 行,每行包含 \(m\) 个正整数,其中第 \(i\) 行第 \(j\) 个数为 \(b_{i,j}\) 。
-
输出格式
输出一行一个整数,表示所求的最大值。
-
样例输入
|
1 2 3 4 5 |
3 4 1 4 2 2 5 1 1 3 3 2 2 2 5 1 |
-
样例输出
|
1 |
11 |
-
样例说明
最优方案如下:以餐馆 \(1\) 为起点,在餐馆 \(1\) 使用第 \(1\) 张餐票、第 \(3\) 张餐票,然后前往餐馆 \(2\) 使用第 \(2\) 张餐票、第 \(4\) 张餐票。
-
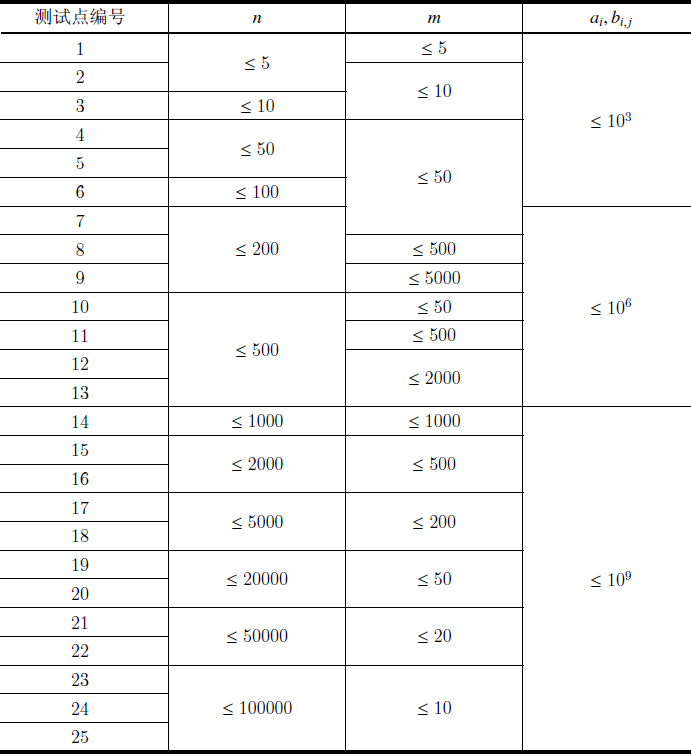
数据规模与约定
对于所有数据,\(nm \leq 10^6\),\(n \geq 2\),\(a_i, b_{i, j} \leq 10^9\) 。
Source:ARC067 F – Yakiniku …