分类： 计算几何

YZOJ P2050 [FJOI2013]圆形游戏

YZOJ P2050 [FJOI2013]圆形游戏

时间限制：8000MS      内存限制：262144KB

难度：\(8.0\)

  • 题目描述

在一个无穷大的桌面上有 \(n\) 个圆形，保证任意两个圆相离或者相含，不存在相切或相交。现在 Alice 和 Bob 在玩一个圆形游戏，以 Alice 为先手，双方以如下步骤轮流游戏：

1，选定一个圆 \(A\)，把 \(A\) 以及所有完全在 \(A\) 内部的圆都删除；

2，如果在自己回合无法找到可删除的圆，则输掉比赛。

假设 Alice 和 Bob 都非常聪明，请问最终谁能够取得胜利？请编程输出最终获胜的人。

  • 输入格式

输入数据的第一行为一个正整数 \(T\)，表示数据组数。

接下来 \(T\) 组数据，对于每组数据，第一行包含 \(1\) 个正整数 \(n\)，表示圆形的个数。

之后 \(n\) 行，每行为 \(3\) 个整数 \(x\)、\(y\) 和 \(r\) ，分别表示圆形的圆心坐标以及圆的半径。

  • 输出格式

假设 Alice 最后获胜，则输出一行 “Alice”（不包括引号），否则输出 “Bob” 。

  • 样例输入

  • 样例输出

  • 数据规模与约定

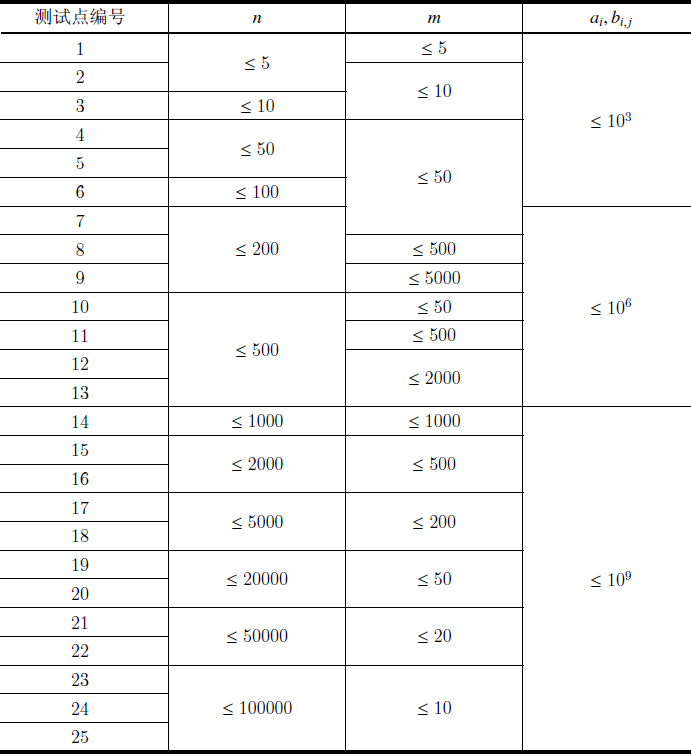
\(100\%\) 的数据满足 \(T \leq 100\)，\(n \leq m20000\)，\(\left|x\right|, \left|y\right|, r \leq 10^8\) 。

 

 

 …

YZOJ P3056 三角形最大面积

YZOJ P3056 三角形最大面积

时间限制：1000MS      内存限制：262144KB

出题人：chj2001         难度：\(4.5\)

  • 题目描述

给定平面上 \(n\) 个点，定义 \(f(A,B,C)=\frac{1}{2} \left| x_A(y_B-y_C)+x_B(y_C-y_A)+x_C(y_A-y_B) \right|\) 。

每次操作都会将坐标系顺时针旋转 \(\frac{\pi}{9}\) 弧度，直到与原坐标系重合。

计算每次操作前 \(f\) 的最大值，并输出所有最大值的总和。

  • 输入格式

第一行输入一个正整数 \(n\)，表示点的数量；

接下来 \(n\) 行，每行两个整数 \(x_i, y_i\) 表示最开始建立的坐标系下点的坐标。

  • 输出格式

输出所有 \(f\) 最大值的总和。

  • 样例输入

  • 样例输出

  • 数据规模与约定

对于 \(100\%\) 的数据，\(3 \leq n \leq 10000, -10000 \leq x_i, y_i \leq 10000\) 。

 

 

 …

YZOJ P2358 [ZJOI 2012]Naive – Matrix

YZOJ P2358 [ZJOI 2012]Naive – Matrix

时间限制：1000MS      内存限制：131072KB

难度：\(7.0\)

  • 题目描述

给出一个 \(R \times C\) 的矩阵，上面有 \(N\) 个 \(0\)，其他的都是 \(1\)，现在给出这些 \(0\) 的位置，要求求出有多少个子矩阵包含至少一个 \(0\) 。

  • 输入格式

第一行输入三个整数 \(R\)、\(C\)、\(N\) 。

接下来 \(N\) 行，每行两个整数 \(x\)、\(y\)，表示 \(0\) 的坐标。

  • 输出格式

输出一个数表示子矩阵的个数。

  • 样例输入

  • 样例输出

  • 数据规模与约定

对于 \(100\%\) 的数据，\(R, C \leq 40000\)，\(N \leq \min\{R \times C,100000\}\)，所有 \(0\) 的位置两两不同且随机生成。

 

 

 

Source: BZOJ 2658…

YZOJ P3791 餐馆

YZOJ P3791 餐馆

时间限制：2000MS      内存限制：524288KB

难度：\(6.0\)

  • 题目描述

在一条东西向的街道上有 \(n\) 个餐馆，从西向东编号为 \(1\) 至 \(n\)，第 \(i\) 个餐馆和第 \(i+1\) 个餐馆的距离为 \(a_i\) 。

吃货小W喜欢到这条街道的餐馆里吃饭。现在，小W得到了 \(m\) 张餐票，每张餐票可以用于在街道上的任一餐馆里吃一餐。在第 \(i\) 个餐馆中，使用第 \(j\) 张餐票吃饭，可以获得的美味度为 \(b_{i,j}\) 。注意，每张餐票最多用一次，但在同一餐馆内可以使用任意多张餐票。

小W打算用完这 \(m\) 张餐票。他可以选择任一餐馆作为起点，每次吃饭时，可以选择一个餐馆，然后从当前位置（上次吃饭的地点，如果不存在则为起点）出发前往该餐馆并用任意一张未用过的餐票吃一餐，直到吃完 \(m\) 餐为止。小W希望最大化每次吃饭的美味度之和减去路上经过的总路程的值。

  • 输入格式

输入第一行包含两个正整数 \(n,m\) 。

第二行包含 \(n-1\) 个正整数 \(a_1,a_2,\cdots,a_{n-1}\) 。

接下来 \(n\) 行，每行包含 \(m\) 个正整数，其中第 \(i\) 行第 \(j\) 个数为 \(b_{i,j}\) 。

  • 输出格式

输出一行一个整数，表示所求的最大值。

  • 样例输入

  • 样例输出

  • 样例说明

最优方案如下：以餐馆 \(1\) 为起点，在餐馆 \(1\) 使用第 \(1\) 张餐票、第 \(3\) 张餐票，然后前往餐馆 \(2\) 使用第 \(2\) 张餐票、第 \(4\) 张餐票。

  • 数据规模与约定

对于所有数据，\(nm \leq 10^6\)，\(n \geq 2\)，\(a_i, b_{i, j} \leq 10^9\) 。

 

 

 

Source：ARC067 F – Yakiniku …