圆规问题
时间限制:1000MS 内存限制:262144KB
-
问题描述
小 C 有一个圆规,他经常用圆规在纸上作图。
有一天,小 C 准备在一个单位网格纸上作一个圆。他以某个格点为圆心,作了一个半径为 \(R\) 的圆。接着,他将圆经过的所有格子涂成黑色。注意:只有圆经过了一个格子的内部才能涂黑,只经过格子的边界不涂黑。小 C 的问题是:对于给定的半径为 \(R\) 的圆,共有多少个格子被涂黑?
这是一个 \(R=10\)的实例:
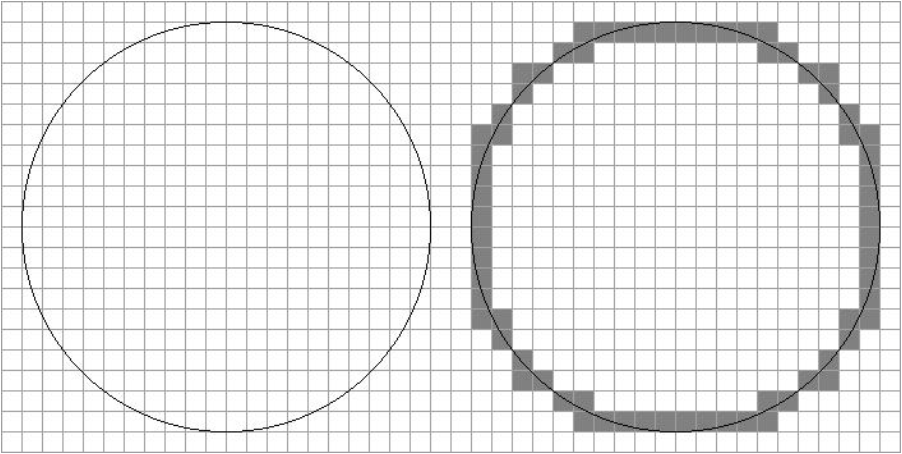
左图为小 C 作的圆,右图是将圆经过的格子涂黑后的图。可以看出,\(R=10\)时,共有 68 个格子被涂黑。
给定\(N\),计算被涂黑的格子数目。
-
输入格式
输入文件包含一个整数\(R\),\(1 \leq R \leq 2,000,000,000\)
-
输出格式
将被涂黑的格子数目输出到文件中。
- 样例输入
|
1 |
10 |
- 样例输出
|
1 |
68 |

不错,可惜这个是人家大神的做法,我的话绝对想不出来。
然后,我想起了一个两年前看到的视频
https://www.youtube.com/watch?v=NaL_Cb42WyY
Translated: https://www.bilibili.com/video/av12131743
首先定义 \(\chi (n) = \left\{ {\begin{array}{*{20}{c}}
0&{n\bmod 2 \equiv 0}\\
1&{n\bmod 4 \equiv 1}\\
{ – 1}&{n\bmod 4 \equiv – 1}
\end{array}} \right.\)
然后,对于半径为\(\sqrt{R}\)的圆,其经过整点个数为\(4 \cdot \sum\limits_{i|R} {\chi (i)} \)
有了这个结论,程序就不难实现。
只需要把\(R\)进行质因数分解,一般质因数分解最差情况下\(O(R)\)当且仅当R为质数,特判一下即可做到\(O(\sqrt{R})\)
然后DFS出\(R^2\)的所有因数(遍历\(R\)的质因数时,把其指数扩大一倍遍历即可),因为\(4 \cdot 10^{18}\)的因数个数仅为\(399\),所以理论下不存在风险。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 |
#include <cstdio> #include <cstdlib> #include <cstring> int kai(const int&a) { if(a%2==0) return 0; else if(a%4==1) return 1; else return -1; } struct _prm { int val;int num; }prm[1050+1]; int base[1050+1][1050+1]; int lprm; int ans,nde; void DFS(int step) { if(step>lprm) { //printf("-----%d %d\n",nde,kai(nde)); //printf("%d,",nde); ans+=kai(nde); return; } for(register int i=0;i<=2*prm[step].num;i++) { if(base[step][i]==0) base[step][i]=base[step][i-1]*prm[step].val%4; //printf("%d -> %d %d ... %d = %d\n",step,prm[step].val,prm[step].num,i,base[step][i]); int bnde=nde; nde*=base[step][i]; nde%=4; DFS(step+1); nde=bnde; } } int main() { for(register int i=0;i<=1050;i++) base[i][0]=1; int R;scanf("%d",&R); register int Rs=R; int nj=2; while(Rs>1) if(Rs%nj==0) { Rs/=nj; if(prm[lprm].val!=nj) prm[++lprm].val=nj; prm[lprm].num++; } else nj++; nde=1; DFS(1); //printf("%d %d --- R\n",nde,ans,R); printf("%lld\n",4*(long long)((long long)R*2-ans)); return 0; } |
base[][]没什么用,忽略吧