YZOJ P3129 [校内训练20170627]跳格子

时间限制：1000MS 内存限制：524288KB

难度：$7.0$

• 题目描述

在一个花园里有一排 $n$ 个格子，这些格子编号为 $1$ 到 $n$ 。袋鼠喜欢在花园的格子上跳跃。

袋鼠的跳跃方式是这样的：一开始，袋鼠位于 $s$ 号格子上，接着它会选择一个尚未经过的格子上跳跃，经过 $n-1$ 次跳跃后，所有格子都被经过了一次，袋鼠的跳跃将结束。袋鼠总是会在 $t$ 号格子结束跳跃。

由于袋鼠中了病毒，所以如果上一步往前跳，那么这一步必须往后跳；反之，若上一步往后跳，那么这一步往前跳。

请问袋鼠有多少种跳跃的方案呢？

形式化地，你需要求出有多少个 $1$ 到 $n$ 的排列 $p_1, p_2, \cdots, p_n$，满足：

1， $p_1=s ，p_n=t$；

2， 对任意 $2 \leq i \leq n-1$，或者 $(p_i-1<p_i) \land (p_i+1<p_i)$ ，或者 $(p_i-1>p_i) \land (p_i+1>p_i)$ 。

• 输入格式

输入共一行，包含三个正整数 $n, s, t$ 。

• 输出格式

输出共一行，包含一个整数，表示跳跃的方案数对 $1,000,000,007$ 取模的结果。

• 样例输入【包含两组样例】

• 样例输出

• 样例 1 说明

从 $2$ 号格子到 $3$ 号格子的跳跃方案有两种，一种是 $2,1,4,3$，一种是 $2,4,1,3$ 。

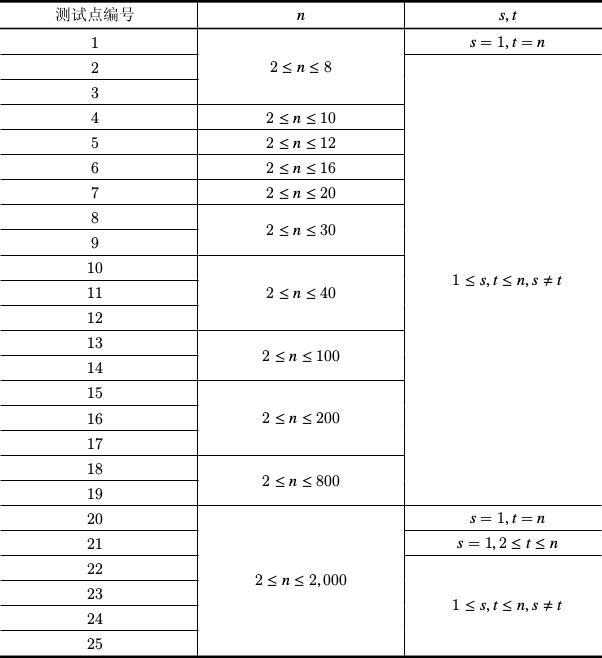
• 数据规模与约定

 

 

 …