浅谈斜率优化——截距优化
最近(两个月前)学习了斜率优化 —— 一种优化 1D1D 动态规划转移方程的高效方法,在较高难度的比赛中是一种十分常见的 DP 优化手段。鉴于我之前(一年前)也稍微接触过一点相关方面的知识,但是完全没有搞懂(太菜了),最近(两个月前)再配合 orzCJK学长 提出的截距优化的思想理念才对于斜率优化问题有了深刻的见解,故在这里对 orzCJK学长 的 斜率优化_截距优化!.pdf 进行详细的解释说明。
首先,1D1D 指的是状态数 \(O(n)\) 转移 \(O(n)\) 的动态规划方程。在满足一些条件的情况下,斜率优化可以将转移的 \(O(n)\) 优化至 \(O(logn)\) 甚至可以到 \(O(1)\) 。这样时间复杂度就由 \(O(n^2)\) 变为 \(O(nlogn)\) 甚至是 \(O(n)\) ,可见斜率优化的高效性。
如果有一个 DP 方程的某个状态为 \(f_i\) ,如果能推导出类似于 \(f_i=c_i + \min\limits_{j<i \land \cdots}{\{a_j + w_i \cdot b_j\}}\) ,那么这个转移方程就可以使用斜率优化进行优化。
然而普通的转移方程并没有什么特殊的地方,使用经典的方法(我也不会)略显繁琐,所以现在我们要赋予它以几何意义。(时刻注意,这个转移方程的意义是对于一个 \(i\) 在 \(j < i\) 范围内寻找 \(j\) 使 \(a_j + w_i \cdot b_j\))最小。)
换一下变量名,设 \(y_j=a_j, k_i=-w_i, x_j=b_j\) ,那么这样需要最小化的式子就变为 \(\underbrace{a_j}_{y_j} – \underbrace{-w_i}_{k_i} \cdot \underbrace{b_j}_{x_j}\) 。这不就是截距 \(b = y – kx\) 吗?!!也就是说,要最小化的就是一条过 \(\left(x_j, y_j\right)\) 且斜率为 \(k_i\) 的直线的截距!
换句话说,把所有对于当前 \(i\) 可转移的 \(j\) 都表示为二维平面上的一个点 \(p_j=\left(x_j, y_j\right)\) ,我们需要做的就是在所有这样的点中,找到一个点,使经过它且斜率为 \(k_i\) 的直线的截距最小!这也是为什么斜率优化就是截距优化的原因,它其实优化的是截距!
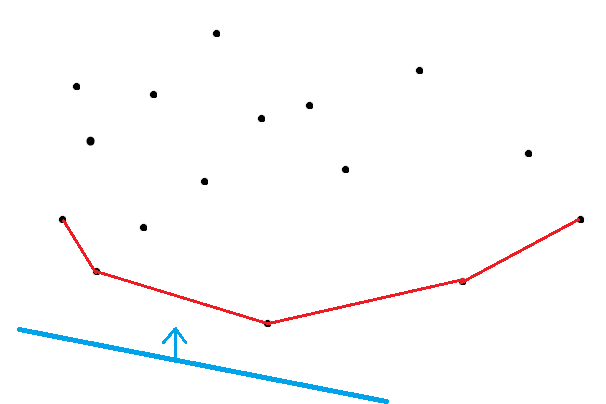
现在想象一条斜率固定的直线从下往上平移,当它第一次经过某个点 \(p_j\) 时,这时的截距肯定取到最小值。那么这个点 \(p_j\) 在什么地方呢?显然,它会在所有 \(p\) 组成的下凸壳上。