YZOJ P1310 [省队训练][NOI模拟7]车的放置
时间限制:1000MS 内存限制:262144KB
难度:\(8.0\)
-
题目描述
有 \(N\) 个 \(1 \times h[i]\) 的矩形小棋盘,底边边长为 \(1\),在一条直线上拼成了一个畸形的棋盘。
高度 \(h[i]\) 给出,第 \(i\) 个矩形的高为 \(h[i]\),例如 \(h = [3, 2, 4, 2]\) 的图形如下: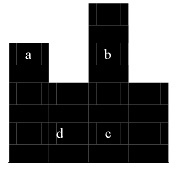
若两个车相互攻击仅当它们在同一列,或在同一行且在这一行它们之间棋盘格子都是存在的,例如上图中 \(a\) 与 \(b\) 是相互不攻击的,\(c\) 与 \(d\),\(b\) 与 \(c\) 均为相互攻击的。
现在要在这棋盘上放置恰好 \(K\) 个相互不攻击的车,问有多少种方案。
-
输入格式
输入第 \(1\) 行包括两个正整数 \(N\),\(K\),表示了棋盘的列数和放的车数。
第 \(2\) 行包含 \(N\) 个正整数,表示了棋盘每列的高度。
-
输出格式
输出包括一个非负整数,表示有多少种放置的方案,输出答案 \(\mod 1000000007\) 后的结果即可。
-
样例输入
|
1 2 |
5 2 2 3 1 2 4 |
-
样例输出
|
1 |
43 |
-
数据规模与约定
对于 \(100\%\) 的数据,有 \(N \leq 500\),\(K \leq 500\),\(h[i] \leq 1000000\) 。